Overview
"Race to Altair" is the first math game I designed, and it's still my favorite. We've played this dozens of times and never seem to get tired of it. Like many race games, it has lots of drama, especially near the end.
Difficulty: 1st grade and up (see tips below for adjusting the level of difficulty).
Number of players: 2-5.
Duration: 20-30 minutes for two players.
Game Materials
At least one set of dragon dice; or, alternatively, one 6-sided die and a set of task cards
One poster-board
One space-themed figure for each person
Making the Game
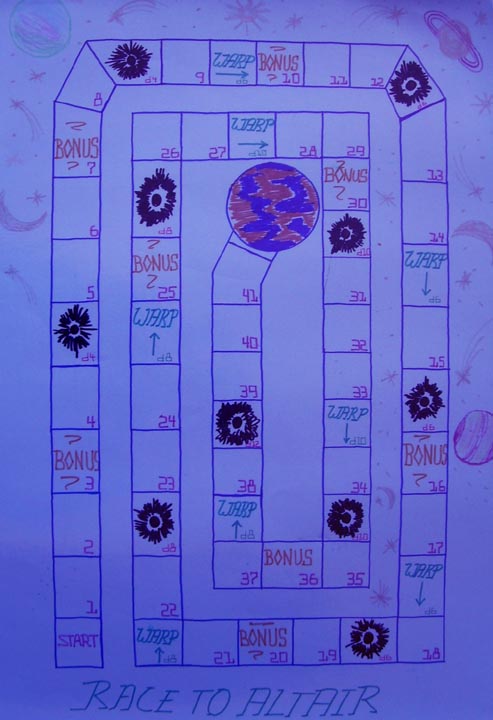
I started with a half-piece of light-blue poster-board for the board, then used a pencil and ruler to draw 58 squares. There 42 regular spaces, including "Start," and 16 special fields (8 black hole, 8 warp; for both, there are two each marked d4, d6, d8, and d10). Eight of the normal spaces are marked "Bonus." Then I went over the design with magic markers and drew the planet Altair at the end (ok, Altair is a star, so, if you like, you can make up a name like "Altair gamma" for the planet, but who wants to play a game called "Race to Altair Gamma"?). Anyway, here is the board:
I also use a smaller piece of poster-board that lists the different kinds of tasks that must be performed. (This is an easy way of adjusting the game's difficulty, about which I'll say more below.) The actual list is just written with magic marker on a white piece of paper. For our current (3rd grade) curriculum, it looks like this:

The different tasks listed here are multiplication (1, 5), subtraction (3, 4), and addition (d20 + d12 for 2, d20 + d12 + d10 for 6). Again, more about this below.
Scenario
The year is 2536, and humankind is colonizing the stars. Recently, we have gotten word of an earth-like planet circling the star Altair, and teams of explorers from various nations are racing to be the first ones to arrive at this planet. To chart the correct course, explorers must solve various problems. Each problem will bring them a step closer to Altair. With good luck, you can also find warp fields that will speed you on your way; but look out, because if you get caught in a black hole, you will be thrown off course and must make up the time you've lost.
Set-Up
Ready your dragon dice and set up the task cards as needed. Put one figure for each player in the "Start" field.
Rules
Players take turns answering questions and (if they answer correctly) moving their figures. The first player to reach Altair wins.
There are several ways to determine which question a player must answer, but I use the task board pictured above. A player starts his turn by rolling a six-sided die. Let's say the number that comes up is 3. Looking at the "3" field on the task board, we can see that the problem type is subtraction (the field is marked with a minus). The player draws from a stack of cards marked with a "-" and turns the card over. The problem "13 - 7 = " is written on the reverse, and the player correctly answers "Six!" If the die roll had been a 1, the player would have drawn from the multiplication deck. If it had been a 2, the player would have rolled d20 and d12, adding the two numbers.
After correctly answering the question, the player rolls the six-sided die again and advances his figure by the appropriate number of spaces.
If the figure lands on a warp space, she rolls the die indicated on the field (d4, d6, d8, or d10) and advances her figure by the appropriate number. If the figure lands on a black hole space, she would also roll the die specified on the field and move backward by the resulting number. However, if she has a bonus card, she can move one space past the black hole without being affected by it. Bonus cards are obtained by landing on a space marked "Bonus."
Now it's the next player's turn ...
Adjusting the Difficulty
"Race to Altair" has been part of our math lessons for three years now. It's still fun to play because we've adjusted the level of difficulty along the way.
In first grade, when we were studying only single-digit addition, there was really no need for the task board. At the beginning of the year, we only rolled two six-sided dice, adding the results. If we hadn't covered a given fact (like 6 + 5) yet, that wasn't really a problem, because the dice make adding visual (my son would start with the six, then add one for every dot on the five, so "Six, seven, eight, nine, ten ... the answer is eleven!"). Once we had mastered all of the addition facts (from 0+0 to 10 +10), we just used two d10 dice instead of the conventional six-sided ones.
In second grade, when we were learning subtraction, it was necessary to stick to just the facts we'd already learned. So, I made up a set of task cards with all of those problems on them; as the year progressed and we learned new facts, I made up more task cards. At this point, I introduced the task board. Since we had also learned column addition, there were three different task types: adding two numbers, adding three numbers, and subtraction.
In third grade, we added multiplication task cards and made the addition problems slightly more challenging.
Using this system, it is also possible to have children at different levels playing the game together, without either boring the advanced students or frustrating the more beginning ones. Simply make one task board for each player.
Other Adjustments
If you find that the games are taking too long, use the d8 or d10 when determining how many spaces to advance your figure. This also introduces more chance into the game.
If you want to minimize the element of chance, don't include so many "Warp" and "Black Hole" spaces, or minimize their effects by using only d4 and d6.