Student Life & Sleep
Jamie Heiden
Jay Jackson
Abstract ~
����������� Our project was designed to examine
the students of Hanover College, and determine how one�s gender, class, and
romantic life could affect their sleeping patterns.� With this information, we could then determine how much sleep
affected what a student�s GPA was.� With
this objective in mind, we set out to determine marginal, joint, and
conditional probabilities for all of our variables, and determine the statistical
significance of a linear regression model for average sleep per night and
GPA.� Our sample was acquired from the
Winter 2001 Student Database, and included all 213 students that adequately
filled out surveys.� These students were
the ones who returned surveys that had gender, class, dating status, and
average sleep per night filled out.�
This information was used to determine who got the most sleep, and what
sleep did for GPA.� We found
conditional, joint, and marginal probabilities for each of our independent
variables (gender, class, and dating status) and sleep and explored for
statistically significant differences in each.�
We discovered a statistically significant difference in average hours of
sleep in freshman and seniors (seniors get more!). �For our sample, there was no difference in average sleep for those
who were dating versus those who were not dating.� There was also no difference in sleep between males and females.� We learned that, in general, more sleep
leads to higher GPA, but sleep is only a very small determinant of the grades
of Hanover students.
Corrections to Data ~
����������� The Winter 2001 Student Database was used for all data.� All of the observations were not useful however, and we found that only 213 surveys contained information that was usable in our statistical tests.� It is important to note that a response of �1� in the gender column meant that a student was female.� Class was represented by a 1,2,3, or 4 - designating freshmen, sophomores, juniors, and seniors, respectively. �And a response of �1� in the dating column meant that a student was currently dating someone.� It was also necessary to alter some of the surveys� responses.� For example, one survey listed that the student got 35 hours a sleep in an average weeknight.� We assumed that this student meant that he or she got 35 hours a sleep in an entire week (that is, a 5-day school week) and changed his response to �7 hours a night� for the school week and his response for average hours of sleep during a weekend night from 15 to 7.5.� We did the same thing for students who listed average sleep during the week as 20 (4 a night) and 15 (3 a night); and sleep during the weekends as 12 (6 a night) and 13 (6.5 a night).� Also, we did not compare sleep to the other variables exactly as it was answered on the survey.� We took the average hours of sleep on a weeknight and multiplied it by five.� We then took average hours of sleep on a weekend at multiplied it by two.� The sum of these two figures was divided by seven, so that we could have a single column of �average sleep per night (for the entire seven-day week)� for each student.� It was much easier to make the needed calculations now that we had this new single column for sleep per night.
Variables ~
Clarification may also be necessary for the table in our spreadsheet found from I218 to P225.� �x� refers to the independent variable in each column.� So, when P(x) is given in row 220, x refers to males in column J, females in column K, and so forth.
Summary Statistics ~
|
NUMBER |
GENDER |
CLASS |
Avg Sleep |
HC_GPA |
DATING |
|
MEAN |
0.5117 |
2.3239 |
7.0092 |
2.9458 |
0.5915 |
|
MEDIAN |
1.0000 |
2.0000 |
7.0714 |
2.9600 |
1.0000 |
|
MODE |
1.0000 |
2.0000 |
7.5714 |
2.5000 |
1.0000 |
|
STDEVS |
0.5010 |
0.9582 |
0.9463 |
0.5199 |
0.4927 |
|
MAX |
1.0000 |
4.0000 |
9.5714 |
3.9900 |
1.0000 |
|
MIN |
0.0000 |
1.0000 |
3.8571 |
1.5000 |
0.0000 |
|
COUNT |
213 |
213 |
213 |
213 |
213 |
����������� We see from our mean gender that more than half of the people in our sample are females (51.17%).� This, however, is to be expected since we know there are more female students at Hanover College then males.� The standard deviation of class is almost one, leading us to believe that our sample had a good mix of all classes, since each standard deviation deviates almost an entire class from the mean.� As predicted, the mean for average sleep per night is right around seven.� However, we can see that students in our sample get as little as four hours of sleep per night and as many as 9 �!� It is interesting to note that the most common response for GPA was nearly a half a point from the mean.� It is also notable that nearly 60% of Hanover students are in a romantic relationship with someone (according to our sample).
How does gender affect
sleep?
��������� The matrix for both gender and sleep is shown below in Table 1.� It is interesting to note that more males got 7+ hours of sleep even though there were fewer males in our sample.� This is reflected in the conditional probability that a student gets 7+ hours of sleep given he is a male (.5962) versus a student who gets 7+ hours of sleep given she is a female (.5413).� We tested for the significance of the difference of these two figures (with Ho: pm-pf = 0 and Ha: pm-pf ≠ 0) and discovered a standard error for pm-pf �of .0669.� This gave us a z-score of .6831, with which we cannot reject the null hypothesis at any confidence level (thus concluding that there is no difference in average sleep per night for males and females).� The covariance and correlation of gender and average sleep can be seen in Tables 5 and 6, respectively.� The covariance for these variables had a negative sign, indicating that there is a negative relationship (females get less sleep than males). But the correlation of -.09776 is not anywhere close to �1 or 1, so we can conclude that the relationship is not strong.
Table 1. Totals by
average hours of sleep per night and gender.
|
|
7+ hours of sleep per night |
<7 hours of sleep per night |
TOTAL |
|
Male (gender=0) |
62 |
42 |
104 |
|
Female (gender=1) |
59 |
50 |
109 |
|
TOTAL |
121 |
92 |
213 |
Marginal
Probabilities:
|
P(M) = 104/213 =.4883 |
P(F) = 109/213 = .5117 |
|
P(7+) = 121/213 = .5681 |
P(<7) = 92/213 = .4319 |
Joint
Probabilities:
|
P(M∩7+) = 62/213 = .2911 |
P(F∩7+) = 59/213 = .2770 |
|
P(M∩<7) = 42/213 = .1972 |
P(F∩<7) = 50/213 = .2347 |
Conditional Probabilities:
|
P(7+׀M) = 62/104 = .5962 |
P(7+׀F) = 59/109 = .5413 |
|
P(<7׀M) = 42/104 = .4038 |
P(<7׀F) = 50/109 = .4587 |
�����������
How does class
affect sleep?
The matrix for the relationship between average sleep per night and class is shown in Table 2.� Nothing stands out as abnormal just looking at the matrix (but that�s why we calculate probabilities!).� Our conditional probabilities point out a seemingly large difference between freshmen and seniors.� The probability that a student got 7+ hours of sleep given that he or she was a freshman was .5238.� If that student was a senior, the probability jumped to .5938.� Again, we conducted a hypothesis test (with Ho: pSr-pFr < 0 and Ha: pSr-pFr > 0) and calculated a standard error of the difference to be .0686.� The z-score we calculated was 1.2986, for which we could�ve rejected the null hypothesis with 80% confidence and conclude that seniors get more sleep than freshmen.� The covariance for these variables (still found in Table 5) is .0596, indicating that the longer you�re at Hanover, the more sleep you�ll get per night.� However, the correlation for sleep and class (Table 6) is only .0660, so the positive relationship between class and sleep we found with the covariance is really not that strong.
Table 2. Totals by
average hours of sleep per night and class.
|
|
7+ hours of sleep per night |
<7 hours of sleep per night |
TOTAL |
|
Freshman (class=1) |
22 |
20 |
42 |
|
Sophomore (class=2) |
54 |
38 |
92 |
|
Junior (class=3) |
26 |
21 |
47 |
|
Senior (class=4) |
19 |
13 |
32 |
|
TOTAL |
121 |
92 |
213 |
Marginal
Probabilities:
|
P(Fr) = 42/213 =.1972 |
P(So) = 92/213 = .4319 |
|
P(Jr) = 47/213 = .2207 |
P(Sr) = 32/213 = .1502 |
|
P(7+) = 121/213 = .5681 |
P(<7) = 92/213 = .4319 |
Joint
Probabilities:
|
P(Fr∩7+) = 22/213 = .1033 |
P(So∩7+) = 54/213 = .2535 |
P(Jr∩7+) = 26/213 = .1221 |
P(Sr∩7+) = 19/213 = .0892 |
|
P(Fr∩<7) = 20/213 = .0939 |
P(So∩<7) = 38/213 = .1784 |
P(Jr∩<7) = 21/213 = .0986 |
P(Sr∩<7) = 13/213 = .0610 |
Conditional Probabilities:
|
P(7+׀Fr) = 22/42 = .5238 |
P(7+׀So) = 54/92 = .5870 |
P(7+׀Jr) = 26/47 = .5532 |
P(7+׀Sr) = 19/32 = .5938 |
|
P(<7׀Fr) = 20/42 = .4762 |
P(<7׀So) = 38/92 = .4130 |
P(<7׀Jr) = 21/47 = .4468 |
P(<7׀Sr) = 13/32 = .4063 |
How does dating affect
sleep?
����������� The matrix showing the relationship between dating and sleep in shown in Table 3.� The only thing that we found interesting was the fact that more people were dating in our sample than not.� There doesn�t appear to be a big difference between those who are dating and not dating with respect to average sleep per night.� However, we conducted a hypothesis test (Ho: pD-pDc = 0 and Ha: pD-pDc ≠ 0) and found the standard deviation for the difference to be .0691 and the associated z-score to be .6816.� Thus, we conclude that we cannot reject the null hypothesis at any level and there is no difference in average sleep per night between those who are dating and those who are not.� The covariance and correlation found in Tables 5 & 6 were .0460 and .0992, respectively.� From these statistics, we conclude that there is� a positive relationship between dating and sleep (if you are dating someone you get more sleep), but alas, this relationship is not strong at all.
Table 3.� Totals by average hours of sleep per night and dating status
|
|
7+ hours of sleep per night |
<7 hours of sleep per night |
TOTAL |
|
Dating (dating=1) |
74 |
52 |
126 |
|
Not Dating (dating=0) |
47 |
40 |
87 |
|
TOTAL |
121 |
92 |
213 |
Marginal
Probabilities:
|
P(D) = 126/213 = .5915 |
P(Dc) = 87/213 = .4085 |
|
P(7+) = 121/213 = .5681 |
P(<7) = 92/213 = .4319 |
Joint
Probabilities:
|
P(D∩7+) = 74/213 = .3474 |
P(Dc∩7+) = 47/213 = .2207 |
|
P(D∩<7) = 52/213 = .2441 |
P(Dc∩<7) = 40/213 = .1878 |
Conditional
Probabilities:
|
P(7+׀D) = 74/126 = .5873 |
P(7+׀Dc) = 47/87 = .5402 |
|
P(<7׀D) = 52/126 = .4127 |
P(<7׀Dc) = 40/87 =.4598 |
How does sleep affect GPA?
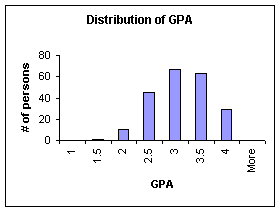
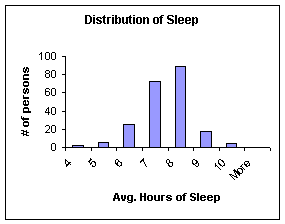
The first step in determining the statistical information was ensuring that our data would be valid in the long run.� For this, we made histograms of both average amount of sleep per night and GPA (as seen in Graphs 1A & 1B) to ensure that they would be normally distributed.� The charts seen were constructed with Excel, and a bin range of one hour was used for sleep and a bin range of .5 points was used for GPA.� Both data were pretty normally distributed, although GPA was slightly skewed to the right (this makes sense because the college makes every attempt to eliminate those students towards the left of the graph).��
Graph 1A.
Graph 1B.
Nothing at all can be made out of just looking at all the points on this graph.� We can see however, that the regression line has a positive slope of .0703.� This is the coefficient for x (b1) as seen in Table 4.� It indicates that for every extra hour of sleep you will get, your GPA will increase .0703 points. The y-intercept lies at 2.4552, making our equation y = .0703x + 2.4552 (as seen on the graph).� The y-intercept (b0) is also represented on our summary output in Table 4, and it tells us that if you never slept, you could still earn a 2.4552 GPA (which, of course, makes no sense at all).� This is because this coefficient acts as a sponge for all of the other variables that contribute to a student�s GPA (e.g., studying, high school GPA, class, etc.).� The R2 is .0164, meaning that approximately 1.6% of the variation in GPAs is determined by the average amount of sleep a student gets per night.� In other words, sleep is not a very good indicator of GPA at all.� This is probably because students that sleep a lot could either be getting well rested to learn; or perhaps they are just sleeping through morning classes.� Likewise, too little sleep could be an indicator of too much partying or a whole lot of studying.
Graph 2.
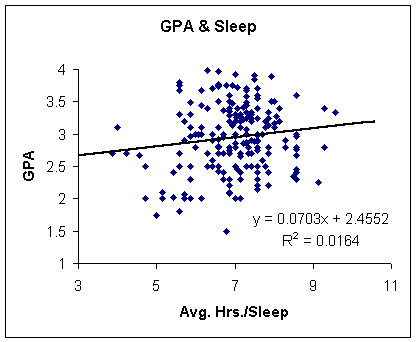
Significance Of This Model~
����������� Before we can pass this model off as a true representation of the relationship between average sleep per night and GPA, we must make sure that the model is statistically sound.� We do this by conducting hypothesis tests on each of the coefficients (b0� & b1) and on the model as a whole (the f-test).� Our null hypotheses for b0� & b1 are as follows:� Ho: b0 = 0 and Ho: b1 = 0.� In other words, we are testing to see if the coefficients actually have an effect on GPA.� Our p-value for b0� is 1.79E-17, indicating that b0 is significant at even the 99% confidence level, because we can reject the Ho that b0 = 0. We can reject the null hypothesis for b1 as well, because its p-value of .060964 falls outside of the 90% confidence level.� This means that b1� is statistically significant at this confidence level, and is a valid indicator of GPA.� Because we used only one variable, our significant f is the same as the p-value for b1.� Thus, we can conclude that our overall model is statistically significant at the 90% confidence level.
Table 4.
|
SUMMARY
OUTPUT |
|
|
|
|
|
|
|
|
|
|
|
|
|
Regression Statistics |
|
|
|
|
|
|
Multiple
R |
0.1280091 |
|
|
|
|
|
R
Square |
0.01638633 |
|
|
|
|
|
Adjusted
R Square |
0.01176843 |
|
|
|
|
|
Standard
Error |
0.51580583 |
|
|
|
|
|
Observations |
215 |
|
|
|
|
|
|
|
|
|
|
|
|
ANOVA |
|
|
|
|
|
|
|
df |
SS |
MS |
F |
Significance F |
|
Regression |
1 |
0.944080954 |
0.944081 |
3.548434 |
0.060964071 |
|
Residual |
213 |
56.66985353 |
0.266056 |
|
|
|
Total |
214 |
57.61393448 |
|
|
|
|
|
|
|
|
|
|
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
|
|
Intercept |
2.45523682 |
0.264142144 |
9.295135 |
1.79E-17 |
|
|
Avg
Sleep |
0.0703234 |
0.03733202 |
1.883729 |
0.060964 |
|
Table 5.
Covariances |
|
|
|
|
|
|
|
|
|
GENDER |
CLASS |
SLEEP1 |
SLEEP2 |
Avg Sleep |
HC_GPA |
DATING |
|
GENDER |
0.24986 |
|
|
|
|
|
|
|
CLASS |
-0.0531 |
0.91384 |
|
|
|
|
|
|
SLEEP1 |
-0.05904 |
0.12501 |
1.19356 |
|
|
|
|
|
SLEEP2 |
-0.01388 |
-0.10408 |
0.08028 |
3.05663 |
|
|
|
|
Avg
Sleep |
-0.04613 |
0.05955 |
0.87548 |
0.93066 |
0.89124508 |
|
|
|
HC_GPA |
0.03226 |
0.07748 |
0.07995 |
0.01175 |
0.06046381 |
0.26905 |
|
|
DATING |
-0.01633 |
0.08537 |
0.01767 |
0.11689 |
0.04602025 |
0.03006 |
0.24162 |
Table 6.
Correlations |
|
|
|
|
|
|
|
|
|
GENDER |
CLASS |
SLEEP1 |
SLEEP2 |
Avg Sleep |
HC_GPA |
DATING |
|
GENDER |
1 |
|
|
|
|
|
|
|
CLASS |
-0.11112 |
1 |
|
|
|
|
|
|
SLEEP1 |
-0.10811 |
0.1197 |
1 |
|
|
|
|
|
SLEEP2 |
-0.01588 |
-0.06227 |
0.04203 |
1 |
|
|
|
|
Avg
Sleep |
-0.09776 |
0.06599 |
0.84884 |
0.56386 |
1 |
|
|
|
HC_GPA |
0.12442 |
0.15625 |
0.14108 |
0.01296 |
0.12347479 |
1 |
|
|
DATING |
-0.06647 |
0.18167 |
0.03291 |
0.13602 |
0.0991711 |
0.1179 |
1 |
Conclusion~
�����������
����������� Hanover College, like many institutions, wants its students to be successful after graduation and stress students� GPAs while in school.� Our sample of 213 students provided us with the information that we used to test how gender, class and dating status affected how many hours of sleep a student gets per night, and in return we learned how average sleep affected GPAs.� Finding that class was the only variable that was statistically significant, meaning that it was the only one that we tested to affect sleep, can allow the administration of Hanover College to assume that seniors are in fact getting more sleep than freshmen.� This piece of information can then be combined with our testing of how sleep affects GPA, and then the administration could expect to find higher GPAs among seniors versus freshmen.� Additionally, students could use this information to determine how to maximize their sleep (to increase their GPA in the long run).� Hanover College, however, should be careful in assuming this because as stated earlier sleep explains only 1.6% of a students GPA leaving 98.4% to be explain by other factors not considered in our model.� If Hanover College could put heavy emphasis on our findings, they could use this information to promote better sleeping habits among students.� Overall, our findings should be taken with a grain of salt because there are many more statistically significant variables that affect GPA than sleep and there are more variables affecting the average hours of sleep a student gets than gender, class, and dating status.